SSA
Gillespie Stochastic Simulation Code
Get the Code
Click the Link for the Github repo of the SSA code
Stochastic Modelling of Chemical Reaction Systems
Chemical reactions are usually modelled by using the ordinary differential equations which considers concentrations of chemical species to be variables that evolves continuously over time. However an underlying assumption using ODE that the system has large number density of molecules such that the effect of fluctuations in number density does not play any significant role in the dynamics of the system. Systems where the number of molecules is low, or where the underlying dynamics of the system is very sensitive to minor fluctuations, the stochastic modelling of chemical kinetics can produce excellent results. In this approach, chemical reactions are modelled using a type of stochastic process called Stationary Markov Jump Process.
Background
The development of various stochastic approaches and it’s application to chemical kinetics primarily started with the work of McQuarrie. Later it is known as Chemical Master Equation. The basic assumption is to consider a system of volume \(\Omega\) at thermal equilibrium at temperature $T$ containing a well-stirred reaction mixture of N chemical species \({S_1, S_2, S_3,...,S_N}\). These chemical species can interact through total $M$ chemical reactions \({R_1, R_2, R_3,...,R_M}\). and with \(X_i(t)\) denoting the population of the species \(S_i\) at time instant \(t\). The system is defined with help of state vectors \(\textbf{X}(t)\), defined as \(\textbf{X}(t) = [X_1(t),X_2(t),...,X_{N-1},X_N]^T\) and all possible combination of the individual populations creates possible state of the system. The system can jump between states using only the reaction channels which are defined as state change vectors. For example if $R_j$ reaction takes place in the system the population of each species changes by the stoichiometric coefficients \(\{ {\nu}_1^{(j)}, {\nu}_2^{(j)},...,{\nu}_{N-1}^{(j)},{\nu}_N^{(j)}\}\). This change is defined by the state change vector \(\nu_j = [{\nu}_1^{(j)}, {\nu}_2^{(j)},...,{\nu}_{N-1}^{(j)},{\nu}_N^{(j)}]^T\). Thus, if the reaction \(R_j\) takes place within the time window $t$ to $t + dt$ then the state of the system transforms from the state \(\textbf{X}(t)\) to the state \(\textbf{X}(t + dt) = X(t) + \nu_j\).
Now, the Prpensity Functions \(a_j(\textbf{x})\) is defined as the transition rate of the jump from state \(\textbf{x}\) to the state \(\textbf{x} + \nu_j\) through the reaction channel \(R_j$ i.e.\ $a_j(\textbf{x})dt\) gives the probability, given \(\textbf{X}(t) = \textbf{x}\),that the reaction \(R_j\) will take place in somewhere in the volume $\Omega$ within the time window \([t, t + dt)\). Taking account all this in mind the conditional probability that the chemical reaction system exists in the state \(\textbf{x}\) at time $t$ starting from the state \(\textbf{x}_0\) at \(t = 0\) is given
\[\label{eqn2} \dfrac{dP(\textbf{x},t|\textbf{x}_0)}{dt} = \sum_{j=1}^{M} a_j(\textbf{x} - \nu_j)P(\textbf{x} - \nu_j,t|\textbf{x}_0) - a_j(\textbf{x})P(\textbf{x},t|\textbf{x}_0)\]This equation is known as the \({\textbf{Chemical Master Equation}}\) (CME) for a reaction system and solution of this equation gives a distribution \(\{(\textbf{x},P(\textbf{x},t|\textbf{x}_0))|\forall{\textbf{x}}\}\) at a time instant \(t\).
Exact form of the Propensity Functions depend on the particular nature of the reaction. Here we will mostly concentrate on three types of reactions i.e.
unimolecular reaction (\(R_\mu : S_i \rightarrow P\)), Bimolecular reaction involving two different type of molecules (\(R_\mu : S_i + S_j \rightarrow P\)) and Bimolecular reaction involving same type of molecules (\(R_\mu : 2S_i \rightarrow P\)). For unimolecular reaction the propensity function is given as \(c_\mu x_j\), where \(c_\mu = k_\mu\). Here \(k_\mu\) is the phenomenological rate constant of the reaction. The expression of \(c_\mu\) is independent of the volume of the system. Similarly, for the bimolecular reaction involving two different type of molecules it is \(c_\mu x_ix_j\), where \(c_\mu = \frac{k_\mu}{\Omega}\) and for a bimolecular reaction involving same molecules it is \(c_\mu\frac{1}{2}x_i(x_i - 1)\), where \(c_\mu = \frac{2k_\mu}{\Omega}\). The bimolecuar reaction rates depend on the collision frequency of the molecules and thus it is related to the number density of the molecules present in the system.
Solving the CME exactly is often difficult for most of the cases and only in a few simple cases exact analytic solution is possible. The main importance of CME lies in the fact that it sets up the background for the exact stochastic simulation of chemical reactions.
Stochastic Simulation Algorithm: Gillespie Algorithm
Gillespie\cite{GILLESPIE1976403} in 1976 introduced a general-purpose technique for simulating the chemical reactions which is knows as the stocastic simulation algorithm(SSA). He proposed a joint probability density function \(p(\tau,j|\textbf{x},t)\) of two new random variables \(\tau\) and \(j\). The function \(p(\tau,j|\textbf{x},t)d\tau\) gives the probability of the event that if the system is in state \(\textbf{x}\) the next reaction \(R_j\) will occur in the system within the time interval \([t+\tau, t+\tau +d\tau)\). He showed that equation \ref{eqn2} together with laws of probability finally leads to this expression of the probability density function \(p(\tau,j|\textbf{x},t)\) as
\[p(\tau,j|\textbf{x},t)d\tau = \textbf{a}_j(\textbf{x})e^{-\textbf{a}_0(\textbf{x})\tau} \label{eqn3}\]where \(\textbf{a}_0(\textbf{x})\) is defined as
\[\textbf{a}_0(\textbf{x}) = \sum_{i=1}^{M=1} \textbf{a}_i(\textbf{x}) \label{eqn4}\]Two random variables \(\tau\) and \(j\) are to be sampled. In his paper, Gillespie introduced two methods: the direct method, where they are sampled using Monte Carlo methods and the next reaction method, which is slightly indirect method. The direct method is usually more efficient and easy to implement. \(\tau\) can be sampled with the following equation:
\begin{equation} \tau = \frac{1}{\textbf{a}_0(\textbf{x})}ln\left( \frac{1}{r_1}\right) \label{eqn5} \end{equation}
where, \(r_1\) is a uniformly distributed random number in range \((0, 1)\). \(j\) is sampled as following way:
\[j = min\Bigg\{j\Bigg| \sum_{j^{\prime}=1}^{j} \textbf{a}_{j\prime}(\textbf{x}) > r_2\textbf{a}_0(\textbf{x}), j \in \{1,2,...,M\} \Bigg\} \label{eqn6}\]here \(r_2\) is also another uniformly distributed random number in range \((0, 1)\). The expression \ref{eqn6} means that \(j\) up the minimum value as an integer of the set {1,2,…,M} such that \(\sum_{j^{\prime}=1}^{j}\) just greater than \(r_2\textbf{a}_0(\textbf{x})\). Now the stochastic search algorithm (SSA) is implemented as follows in Python:
- Input: \(\textbf{x}_\textbf{0}, \{\nu_j\}, \{k_j\}, T, \Omega\), number of Monte Carlo steps.
- Initialize \((t = 0, \textbf{X}(t) = \textbf{x}_{\textbf{0}})\)
- Begin Loop
- Calculate: \(\{ a_{j^{\prime}} \}\) according to the reaction order.
- Calculate: \(\textbf{a}_{\textbf{0}}\)
- Generate two random numbers: \((r_1, r_2)\)
- Sample random variables: \((\tau, j)\)
- Update: \(t = t + \tau\) and \(X(t + \tau) = X(t) + \nu_j\)
- Print: \((t, X(t))\)
- Continue: up to Monte-Carlo steps are done.
- Break the loop when required number of Monte Carlo Steps are done
In the above implementation rate constants of the elementary reactions (\(k\)) are required. We calculated the rate constants using the \(\textbf{Eyring Equation}\):
\begin{equation} k = \frac{k_BT}{h}e^{-\frac{\Delta G^{\dagger}}{RT}} \label{eqn7} \end{equation}
\(\Delta G^{\dagger}\) are calculated as \(\Delta G^{\dagger} = [G(TS) - G(Reactant)]\) for each elementary reaction.
Increasing the temperature also increases the Gibbs free energy value of each species. We did not consider it here because we assume increasing the temperature elevates the Gibbs free energy of all the species roughly equal so that the relative energy difference remains more or less identical. Increasing temperature of the stochastic simulation will affect the reaction rate via \emph{\textbf{Eyring Equation}}.
Features of Our Code
- This SSA implementation is more of a Chemist way in reaction mechanism study.
- Written in Python, easy to understand and modify accordingly.
- Restart Option, Convert checkpoint file to csv file etc.
- Merge the results of two different simulation run.
- Integrated analysis with Pandas and Matplotlib for quick analysis.
- Output is in csv format so can be plotted in any plotting tool.
Input file for SSA code
YAML format is used to provide the inputs to the SSA code. A sample input file can be generated from the command line
python kinetics.py --sample_yaml conf.yaml
An example input file is provided here (used in the publication).
Temp: 373 # Set Temperature of the simulation in Kelvin
Steps: 5000000 # Number of Monte-Carlo Steps
Initial_pop: # Initial population of the reactants
A0 : 1000
PH3: 4000
A1 : 0
A2 : 0
A3 : 0
A4 : 0
A5 : 0
A6 : 0
A7 : 0
A8 : 0
A9 : 0
A10: 0
A11: 0
A12: 0
A13: 0
A16: 0
A14: 0
A15: 0
A17: 0
A18: 0
A19: 0
A20: 0
A21: 0
A23: 0
Stoichiometry:
#- [[G],[A0,PH3,A1,A2,A3,A4,A5,A6,A7,A8,A9,A10,A11,A12,A13,A16,A14,A15,A17,A18,A19,A20,A21,A23]]
- [[5.00], [-1,-1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[2.05], [ 1, 1,-1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[1.76], [ 0, 0,-1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[11.55], [ 0, 0, 1,-1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[5.00], [ 0,-1, 0,-1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[2.98], [ 0, 1, 0, 1,-1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[5.00], [ 0,-1, 0,-1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[1.45], [ 0, 1, 0, 1, 0,-1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[2.80], [ 0, 0, 0, 0,-1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[13.29], [ 0, 0, 0, 0, 1, 0,-1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[0.78], [ 0, 0, 0, 0, 0,-1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[17.88], [ 0, 0, 0, 0, 0, 1, 0,-1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[5.00], [ 0,-1, 0, 0, 0, 0,-1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[3.57], [ 0, 1, 0, 0, 0, 0, 1, 0,-1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[5.00], [ 0,-1, 0, 0, 0, 0,-1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[1.05], [ 0, 1, 0, 0, 0, 0, 1, 0, 0,-1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[5.00], [ 0,-1, 0, 0, 0, 0, 0,-1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[3.27], [ 0, 1, 0, 0, 0, 0, 0, 1, 0, 0,-1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[9.52], [ 0, 0, 0, 0, 0, 0, 0, 0,-1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[4.38], [ 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0,-1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[11.4], [ 0, 0, 0, 0, 0, 0, 0, 0, 0,-1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[20.6], [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0,-1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[8.79], [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,-1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[2.08], [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0,-1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[5.00], [ 0,-1, 0, 0, 0, 0, 0, 0, 0, 0, 0,-1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[3.88], [ 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0,-1, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[5.00], [ 0,-1, 0, 0, 0, 0, 0, 0, 0, 0, 0,-1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0]]
- [[2.25], [ 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0,-1, 0, 0, 0, 0, 0, 0]]
- [[5.00], [ 0,-1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,-1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0]]
- [[3.04], [ 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0,-1, 0, 0, 0, 0, 0]]
- [[5.00], [ 0,-1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,-1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0]]
- [[4.35], [ 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0,-1, 0, 0, 0, 0]]
- [[5.00], [ 0,-1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,-1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0]]
- [[11.06], [ 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0,-1, 0, 0, 0, 0, 0, 0, 0]]
- [[5.00], [ 0,-1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,-1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[8.98], [ 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0,-1, 0, 0, 0, 0, 0, 0, 0, 0]]
- [[7.48], [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,-1, 0, 0, 0, 0, 0, 1, 0, 0, 0]]
- [[8.28], [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0,-1, 0, 0, 0]]
- [[10.14], [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,-1, 0, 0, 0, 0, 1, 0]]
- [[30.90], [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0,-1, 0]]
- [[11.91], [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,-1, 0, 0, 0, 0, 1]]
- [[20.29], [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0,-1]]
- [[8.89], [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,-1, 0, 0, 1, 0]]
- [[14.94], [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0,-1, 0]]
- [[7.94], [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,-1, 0, 0, 0, 0, 0, 0, 1, 0]]
- [[18.76], [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0,-1, 0]]
- [[3.14], [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,-1, 0, 0, 0, 0, 1, 0, 0]]
- [[10.14], [ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0,-1, 0, 0]]
Explanation of the input file
Temp is the temperature setting for the simulation. Steps are the number of Monte-Carlo step for the simulation. Initial_pop is the population of all the species at the beginning of the simulation. In the above example only A0 and PH3 species exists at the beginning of the reaction. Populations of the other species involved in the whole reaction are set to zero.
Now the Stoichiometry section contains the reaction vector. e.g. the first line is
Stoichiometry:
#- [[G],[A0,PH3,A1,A2,A3,A4,A5,A6,A7,A8,A9,A10,A11,A12,A13,A16,A14,A15,A17,A18,A19,A20,A21,A23]]
- [[5.00], [-1,-1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
Here 5.00 is the activation Gibbs free energy (in kcal/mol) of a particular elementary reaction (for this case A0 + PH3 --> A1). -1 indicates that this particular species is consumed in this reaction channel e.g in this case both A0 and PH3 and 1 indicates the species which is formed , in this case A1. AS others species are not involved in this reaction path so they are set to zero. The total number of items in this list
Stoichiometry:
#- [[G],[A0,PH3,A1,A2,A3,A4,A5,A6,A7,A8,A9,A10,A11,A12,A13,A16,A14,A15,A17,A18,A19,A20,A21,A23]]
[-1,-1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
has to be same as the total number of species in the Initial_pop section. The next line in the input file
Stoichiometry:
#- [[G],[A0,PH3,A1,A2,A3,A4,A5,A6,A7,A8,A9,A10,A11,A12,A13,A16,A14,A15,A17,A18,A19,A20,A21,A23]]
- [[2.05], [ 1, 1,-1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]
is the reverse of the above reaction (A0 + PH3 <-- A1). In this way the reaction vectors are set up for all the elementary reaction involved in the whole reaction system.
Some sample results
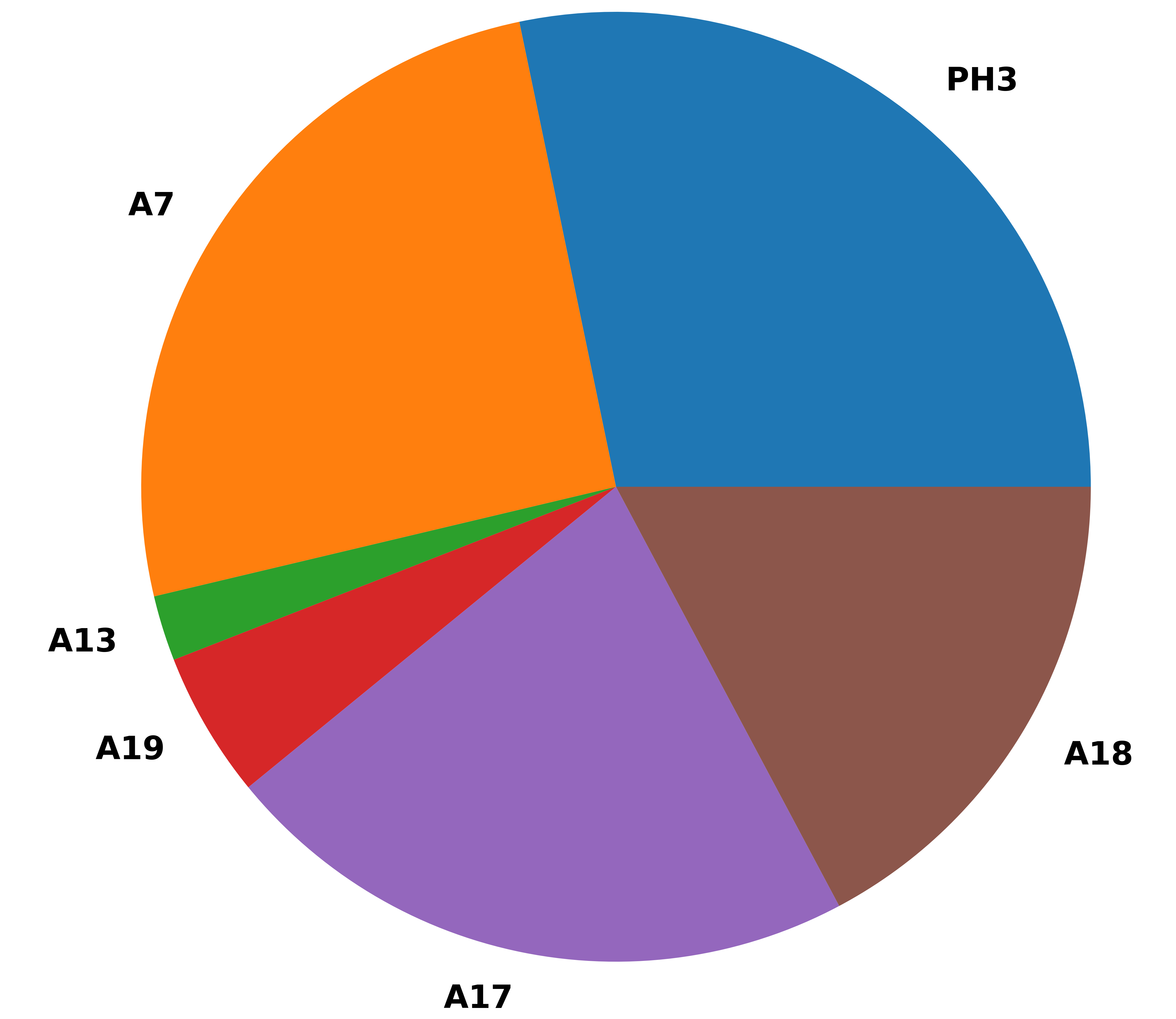
Enjoy !!!